本事例では全固体電池に使用される固体電解質中のLiイオンの拡散を、第一原理計算を用いて解析した事例を紹介します。第一原理計算を用いて固体中のイオン拡散を解析する場合、通常は第一原理分子動力学法(第一原理MD)を用いてイオンの運動を直接追跡する方法が用いられます [1]。しかし、第一原理MDを用いてイオンの拡散経路を完全に再現するためには、長時間のMD計算の結果を用いてイオン分布の統計的に評価しなければならないため、非常に計算コストがかかります。そこで、本事例では溶液論である3D-RISM法と第一原理計算を連成させた3D-RISM-SCF法 [2, 3] を用いて、簡便に固体電解質中のLiイオンの拡散分布を評価しました。
1.計算モデル
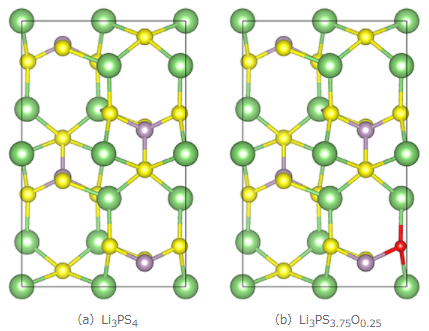
ここでは固体電解質としてLi3PS4を検討しました。また、Li3PS4に対して一部酸素をドープしたLi3PS3.75O0.25も併せて解析し、元素ドープがLiイオンの拡散に与える影響を検討しました。図1に本事例で用いた計算モデルを示します。
計算手順として、図1の計算モデルを用いて構造最適化を行ったのち、計算モデルからLiを削除し、Liイオンを溶媒種として3D-RISM-SCF法よりLiイオンの分布を解析しました。
2.計算条件
表1に本事例における計算条件を示します。
表1 計算条件
| 項目 | 説明 |
|---|---|
| 使用ソルバー | q-e-qe-6.5-rism [4] |
| 擬ポテンシャル | Li:Li_pbe_gbrv_v1.4.upf P:P_pbe_gbrv_v1.5.upf S:S_pbe_gbrv_v1.4.upf O:O_pbe_gbrv_v1.2.upf |
| カットオフ 波動関数 | 40 Ry |
| カットオフ 電子密度 | 200 Ry |
| k点 | 3×3×3 |
| 収束閾値 | 10-8(SCF), 10-4(Force) |
| Mixingパラメータ | 0.3 |
| RISM条件 | Closure: Kovalenco-Hirata(KH) 溶媒温度:300K, 600K, 900K 溶媒密度カットオフ:160 Ry 溶質LJ力場:UFF 溶媒LJ力場:OPLSAA |
3.計算結果
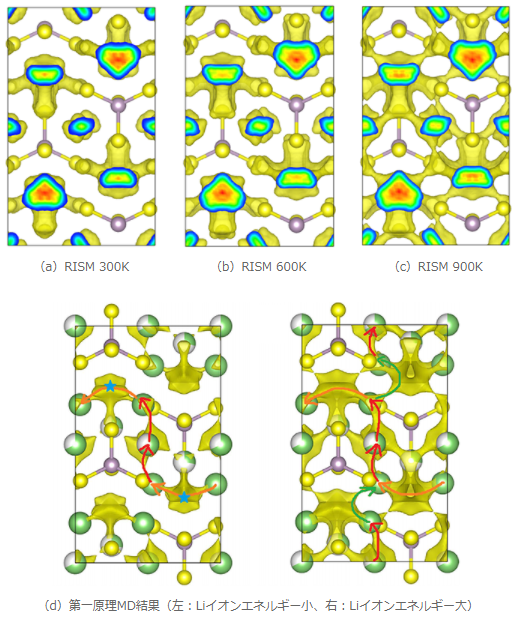
図2にLi3PS4におけるLiイオン分布の3D-RISM-SCF計算結果と第一原理MDによる文献結果 [1]を示します。3D-RISM-SCF計算結果は第一原理MDの計算結果をよく再現していることが分かります。第一原理計算ではLiイオンに与える運動エネルギーとLiイオンの拡散パスの対応を解析していますが、3D-RISM-SCFでは溶媒種の温度を変えることで同様の解析が可能となっています。また、第一原理MDでは数千ステップ以上の計算を要しますが、3D-RISM-SCF法ではエネルギー1点計算の結果のため、計算コストを大幅に削減した計算となっています。
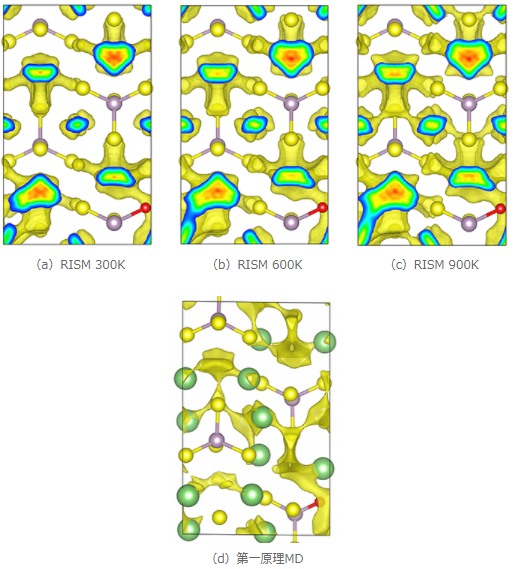
また図3にLi3PS3.75O0.25におけるLiイオン分布の3D-RISM-SCF計算結果と第一原理MDによる文献結果 [1] を示します。Li3PS4の場合と同様に3D-RISM-SCF法の計算結果は第一原理MDの計算結果をよく再現しており、元素ドープがLiイオン拡散に与える影響を再現できていることが確認できました。
4.計算時間とコスト
最後に本計算の実施にかかった計算時間とコスト表2に示します。
表2 計算時間と計算コスト(セービングノード36コアを使用)
| 計算モデル | 計算時間 | 金額[ドル] |
|---|---|---|
| Li3PS4 溶媒温度300K | 1h55m | 2.5 |
| Li3PS4 溶媒温度600K | 1h15m | 2.3 |
| Li3PS4 溶媒温度900K | 58m | 2.0 |
| Li3PS3.75O0.25 溶媒温度300K | 2h18m | 2.8 |
| Li3PS3.75O0.25 溶媒温度600K | 1h27m | 2.3 |
| Li3PS3.75O0.25 溶媒温度900K | 1h7m | 2.1 |
5.参考文献
[1] R. Xiao, H. Li and L. Chen, “High-throughput design and optimization of fast lithium ion conductors by the combination of bond-valence method and density functional theory”, Scientfic Reports, 5, 1 (2015)
[2] A. Kovalenko and F. Hirata, “Self-consistent description of a metal–water interface by the Kohn–Sham density functional theory and the three-dimensional reference interaction site model”, J. Chem. Phys. 110, 10095 (1999)
[3] S. Nishihara and M. Otani, “Hybrid solvation models for bulk, interface, and membrane: Reference interaction site methods coupled with density functional theory”, Phys. Rev. B 96, 115429 (2017)
[4] Satomichi Nishihara's git repository(https://gitlab.com/nisihara1/q-e)