ここでは金属結晶の仕事関数の計算方法を紹介します。
下記の手順で行います。
1. 結晶構造の最適化
2. スラブモデル作成
3. ESMモデル作成
4. ESM法を適応した構造最適
5. 仕事関数の値比較
1.結晶構造の最適化
まず初めにMaterial Projects から取得したBCC構造のLiで計算を行います。計算ソフトには、Quantum ESPRESSOを使用しました。
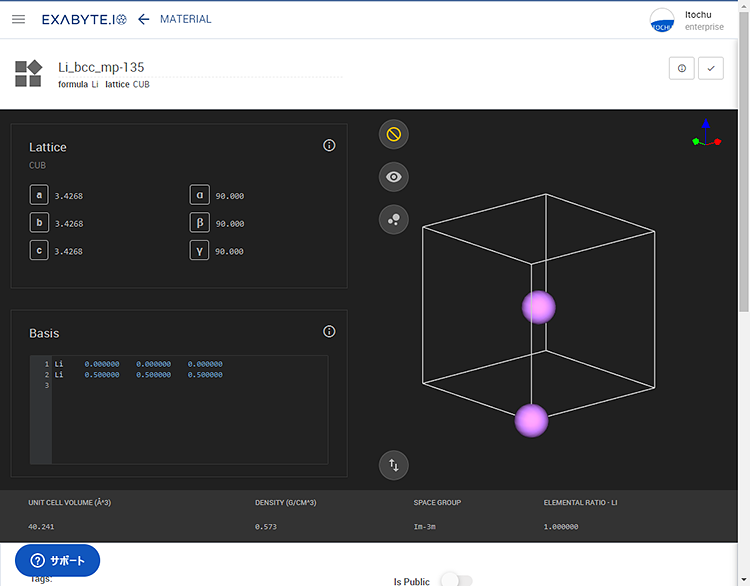
図1 BCC構造のLiの結晶構造
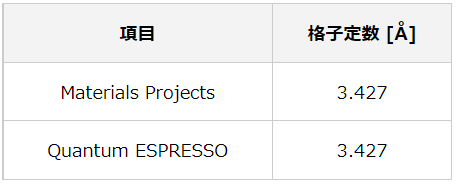
表1 Materials ProjectsとQuantum ESPRESSOの格子定数
2.スラブモデル作成
最適化された結晶構造を基に、金属スラブモデルを作成します。Exabyte.ioに搭載されているスラブモデルもしくは、NanoLaboを用いて作成することも可能です。
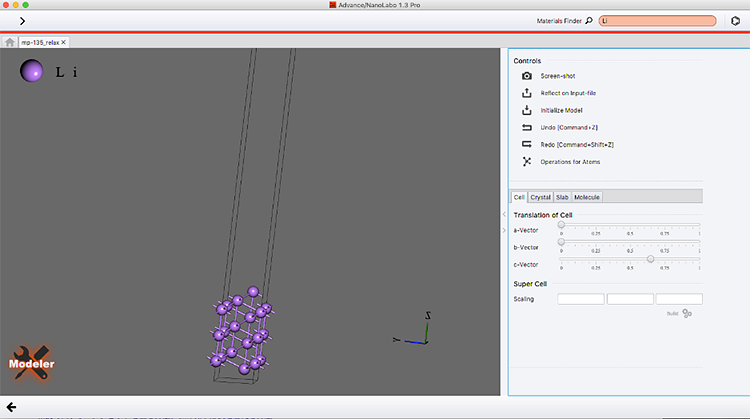
図2 NanoLaboでスラブモデルを作成した様子
ここでは、100面、110面、111面を作成しました。
※NanoLaboをExabyte.io上で使用することも可能です。
3.ESMモデル作成
Quantum ESPRESSOのESM法の機能を使うことで、真空層を多く取らずに精度よく求めることが可能です。そのためここでは、Quantum ESPRESSOのESM法の機能で計算するためのモデルを作成します。モデルは、「Boundary Conditions」から作成します。今回はTypeにbc3を選択しました。
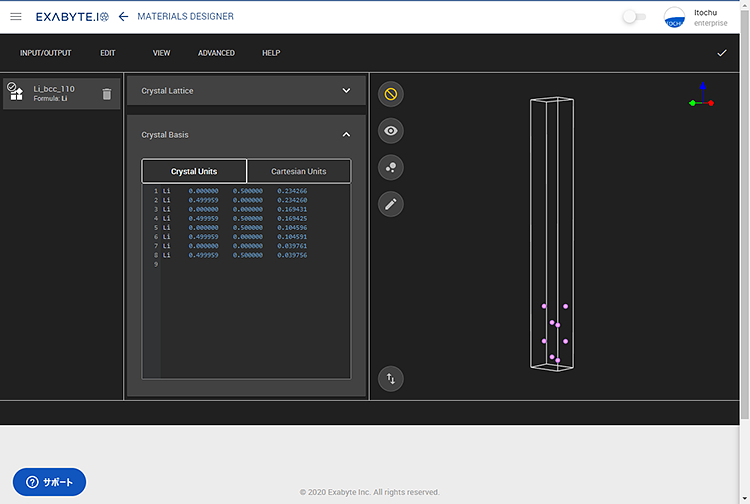
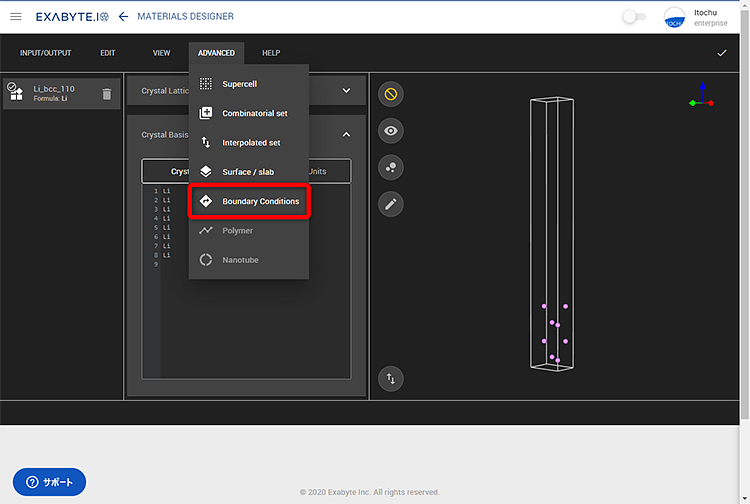
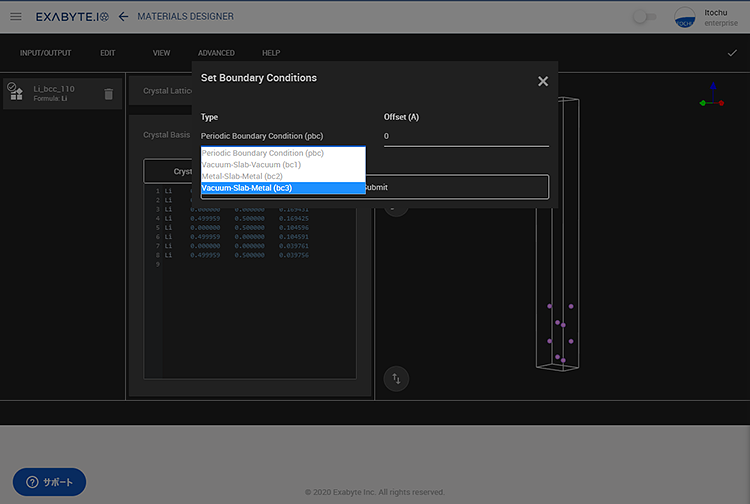
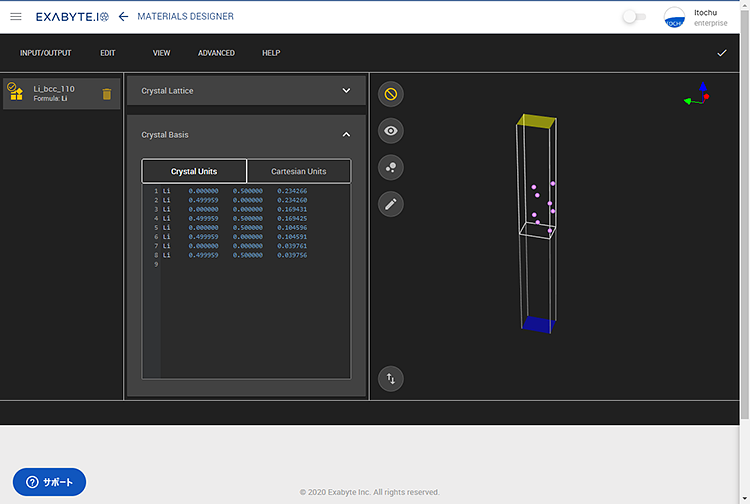
図3 モデルの作成例
作成したESMモデルを保存します。
4.ESM法を適応した構造最適
Exabyte.ioでは、ESM法を用いる計算ワークフローが用意されています。今回は、“Effective Screening Medium (ESM) Relax”を使用します。
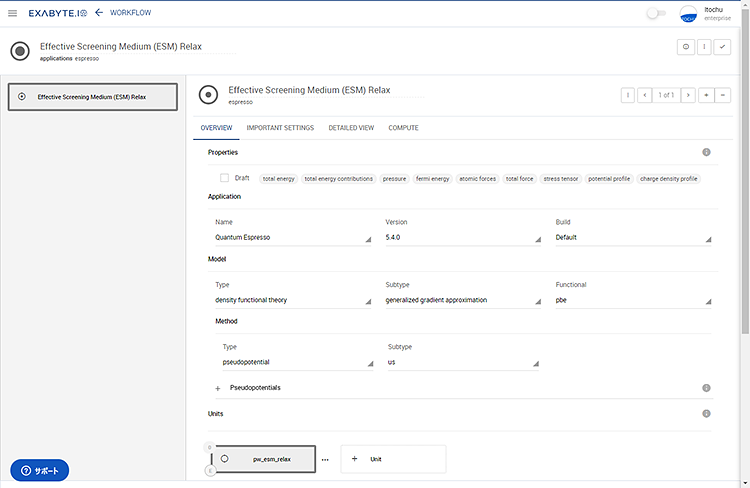
図4 ESM法を用いた構造最適化のワークフロー
5.仕事関数の値比較
計算結果は、下記のように表示されます
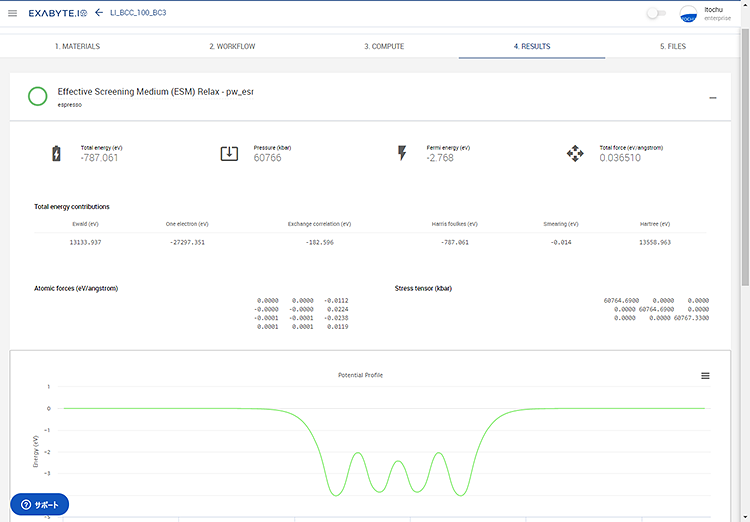
図5 計算結果画面
ESM法を使用することで、端のポテンシャルがゼロの値になるため、フェルミ準位の符号を変えた値が仕事になります。
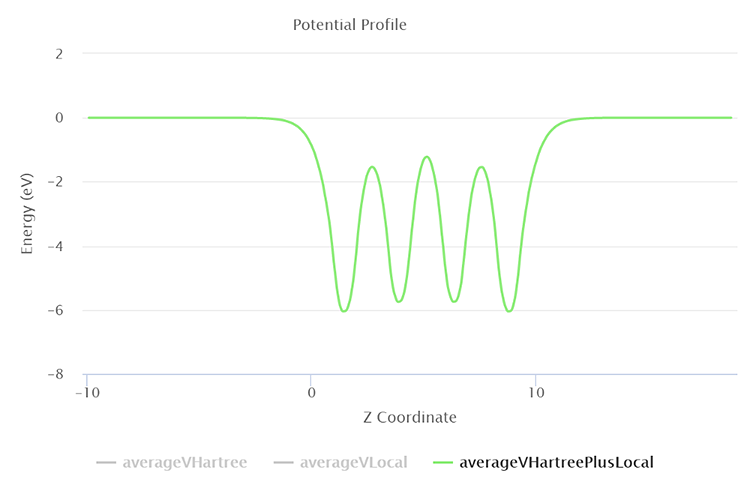
図6 Exabyte.ioで表示されるポテンシャルエネルギー図
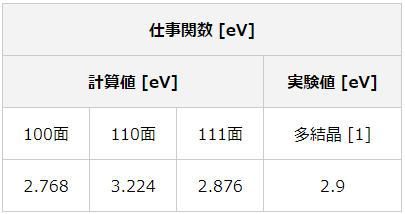
各方位面での仕事関数の値と実験値を比較した結果を示します。
表2 各方位面での仕事関数の値と実験値の結果
計算結果は実験値に近い値を示しています。すべての面の平均値は2.95 eVになり、さらに実験値に近い値になっています。
[1] A.P.Ovchinnikov and B.M.Tsarev,Sov.Phys.-Solid State 9 (1968) 2766