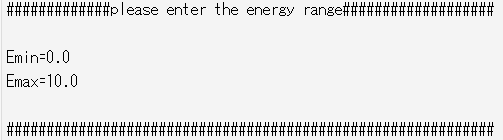III-V族半導体はダイオードなどの発光素子の素材として用いられるため、その光学特性を第一原理計算から予測することは有用と考えられます。ここではSiおよびIII-V族半導体であるGaAsの誘電関数を、第一原理計算を用いて計算する方法を説明します。誘電関数からは吸収スペクトル、誘電率、および反射率などの光学特性を評価することも可能です。
1.計算モデル作成
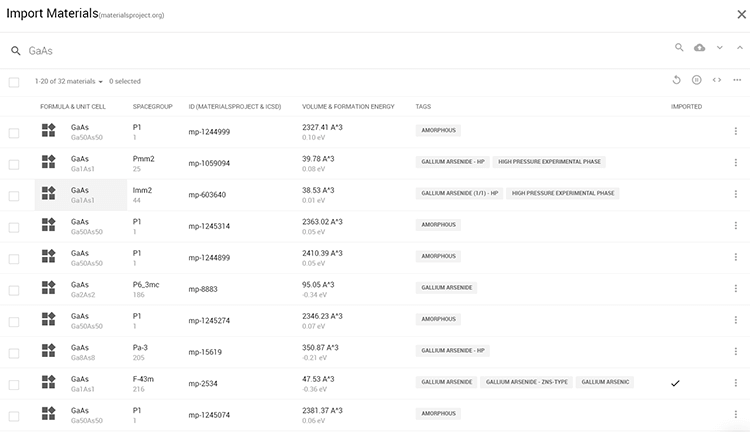
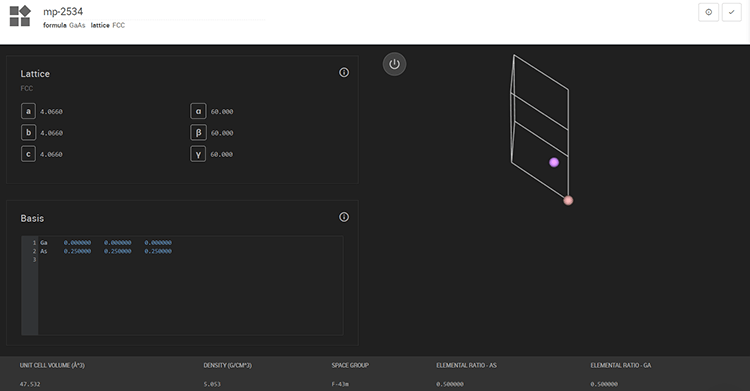
Import Materials画面で物質名SiおよびGaAsを検索することで簡単に必要な結晶構造を入手することができます(図1および図2)。
2.電子誘電関数計算の実行
電子誘電関数はQuantum Espressoの誘電関数計算機能であるepsilon.xを用いて計算します。epsilon.xで誘電関数を計算するための計算条件を表1に示します。
表1 誘電関数の計算条件
| 項目 | 詳細 |
|---|---|
| 擬ポテンシャル | Si_ONCV_PBE_sr.upf Ga_ONCV_PBE_sr.upf As_ONCV_PBE_sr.upf |
| カットオフ 波動関数 | 55 Ry |
| カットオフ 電子密度 | 220 Ry |
| k点 | scf:4×4×4 nscf:12×12×12 |
| 収束閾値 | 10-10 |
| バンド数 | 20 |
また、PBE計算におけるバンドギャップ(bg)の過小評価は、誘電関数の精度に影響を与える可能性があるため、実験値のバンドギャップと計算結果のバンドギャップの差の分だけ誘電関数を補正する方法(シザー近似)も検討しました。ただし、常にバンドギャップの実験値が得られるとは限らないため、Hybrid汎関数法HSEを用いて計算されたバンドギャップを用いて補正する場合についても検討しました。HSE法の計算条件を表2に示します。
表2 HSE法の計算条件
| 項目 | 詳細 |
|---|---|
| 擬ポテンシャル | Si_ONCV_PBE_sr.upf Ga_ONCV_PBE_sr.upf As_ONCV_PBE_sr.upf |
| カットオフ 波動関数 | 55 Ry |
| カットオフ 電子密度 | 220 Ry |
| k点 | scf:4×4×4 |
| 収束閾値 | 10-10 |
| バンド数 | 20 |
表3にPBEおよびHSEにより計算されたバンドギャップと実験値のバンドギャップを示します。HSEおよび実験値とPBEのバンドギャップとの差を用いて誘電関数を補正します。
表3 バンドギャップの計算結果
2.1 吸収スペクトル
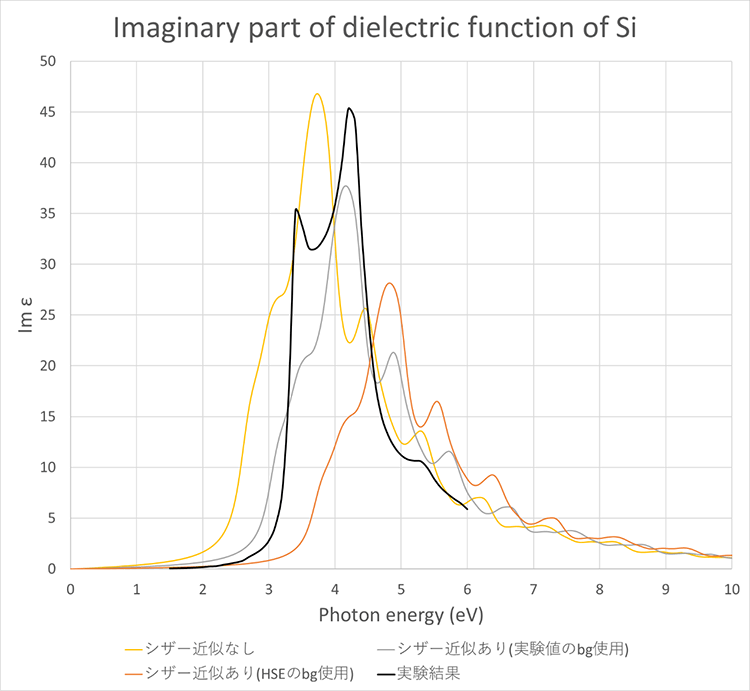
図3、図4に誘電関数の虚部の計算結果を示します。誘電関数の虚部は吸収スペクトルに対応します。シザー近似を行うことで、スペクトルの吸収位置が実験結果に近づくことが確認できます。
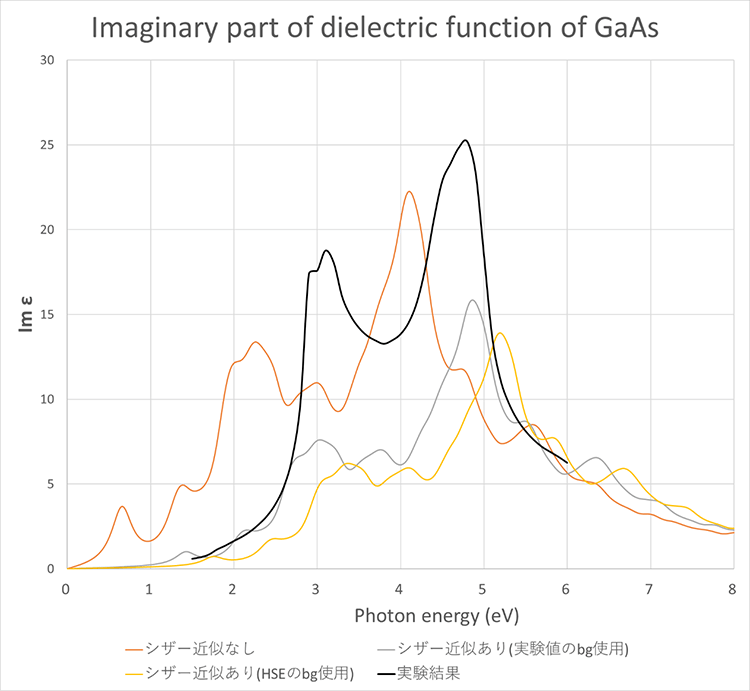
2.2 誘電率
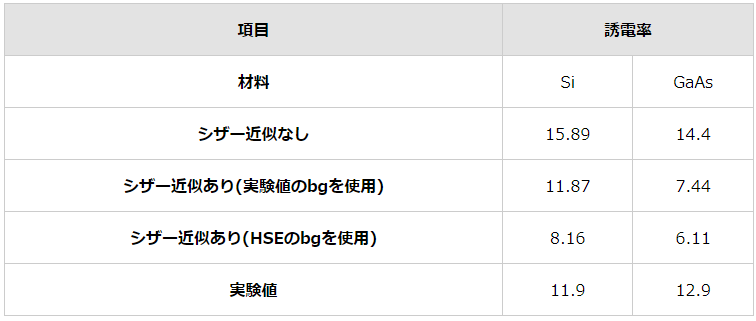
また、図5、図6に誘電関数の実部の計算結果を示します。Photon energyが0の時の誘電関数の値から誘電率を評価することができます。表4に誘電率の計算結果を示します。誘電関数の形状(ピーク位置など)はシザー近似を行うことで実験結果に近くなります。一方で、誘電関数の値はSiではシザー近似により改善されましたが、GaAsでは改善されない結果となりました。
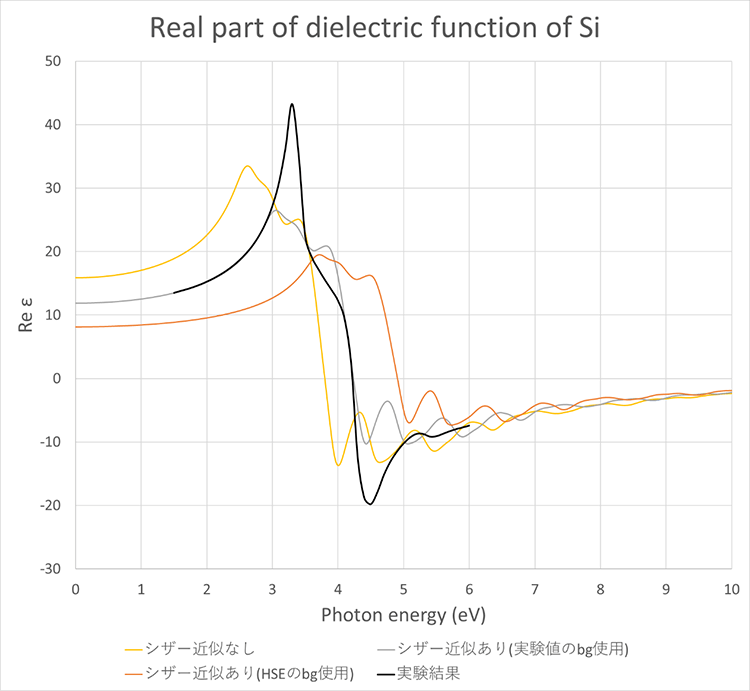
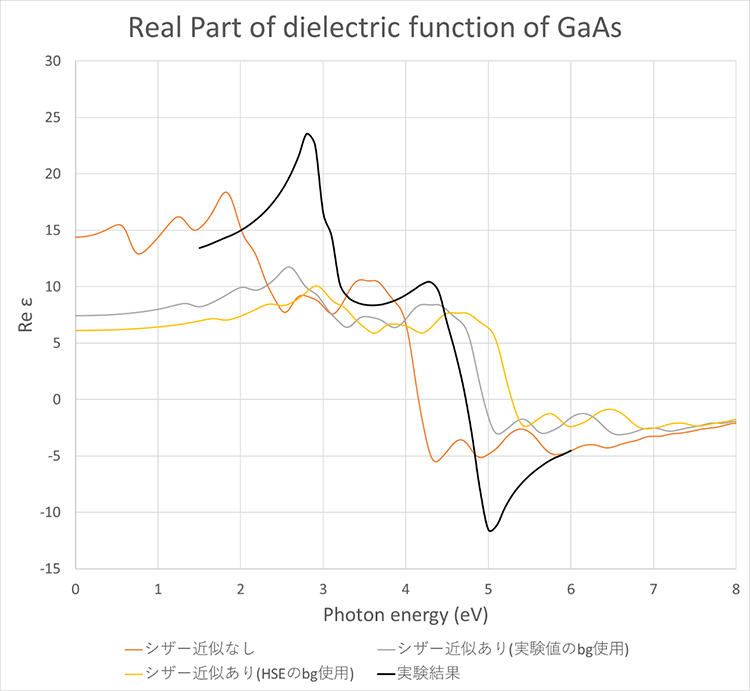
表4 誘電率の計算結果
2.3 反射率
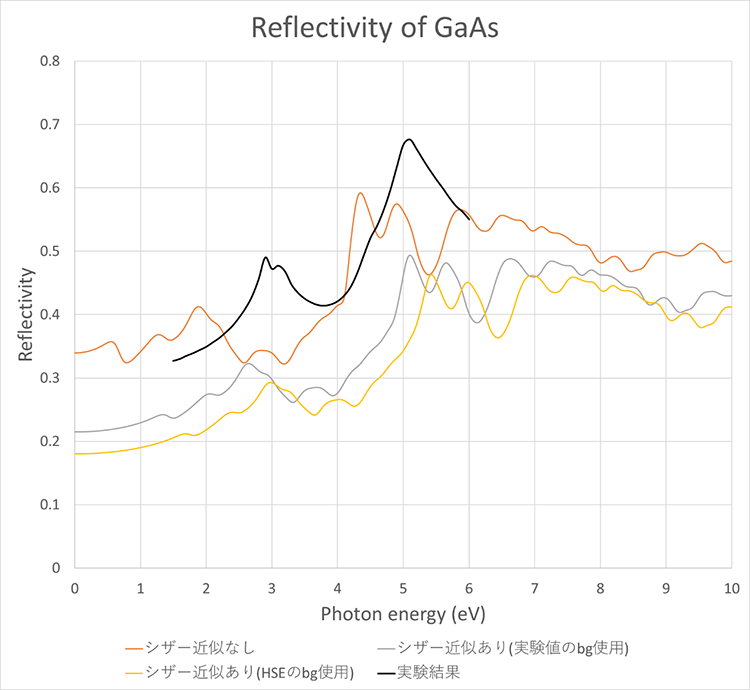
続いて、図7、図8に反射率の計算結果を示します。シザー近似を行うことで、反射率の形状(ピーク位置など)が実験結果に近づくことが確認できます。また、Siの場合はシザー近似を行うことで、反射率の値も実験結果に近い結果を得ることができました。
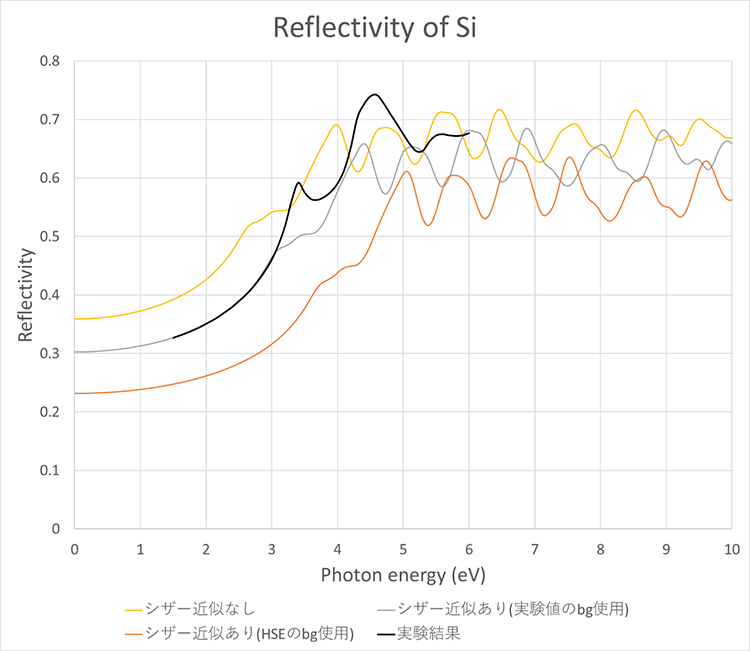
3.電子誘電関数計算のワークフローについて
Quantum Espressoのepsilon.xで電子誘電関数を計算するためのワークフロー(図9)と詳細情報を表5に示します。
表5 誘電率計算のワークフロー情報
また、グラフ出力のエネルギー範囲はmk_graphフロー中にエネルギーの下限値と上限値を入力することで設定可能です(図10)。
図10 グラフ描画実行フローmk_graph中のエネルギー範囲の入力欄
Eminがエネルギー下限値、Emaxがエネルギー上限値に対応 (eV単位)
電子誘電関数のワークフローはBankから「electronic_dielectric_function(QE6.3)」を取得してご利用ください。
4.計算時間とコスト
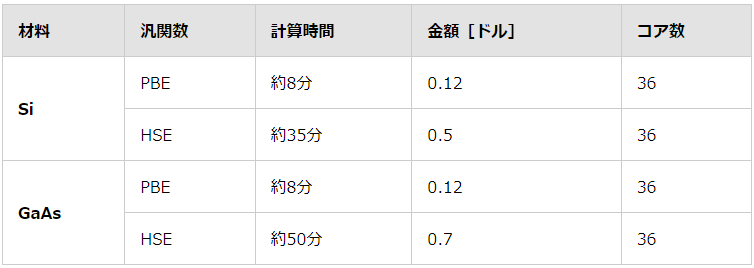
最後に本計算の実施にかかった計算時間とコスト表6に示します。
表6 電子誘電関数計算の計算時間とコスト(セービングノードを使用)